BFS and DFS in Graph

Posted on Edited on In , Views:

What is Graph Data Structure

A Graph is a non-linear data structure consisting of vertices and edges. The vertices are sometimes also referred to as nodes and the edges are lines or arcs that connect any two nodes in the graph. More formally a Graph is composed of a set of vertices( V ) and a set of edges( E ). The graph is denoted by G(E, V).

Components of a Graph

  • Vertices are the fundamental units of the graph. Sometimes, vertices are also known as vertex or nodes. Every node/vertex can be labeled or unlabelled.
  • Edges are drawn or used to connect two nodes of the graph. It can be ordered pair of nodes in a directed graph. Edges can connect any two nodes in any possible way. There are no rules. Sometimes, edges are also known as arcs. Every edge can be labeled/unlabelled.

DFS

[Leetcode 399] Evaluate Division

You are given an array of variable pairs equations and an array of real numbers values, where equations[i] = [Ai, Bi] and values[i] represent the equation Ai / Bi = values[i]. Each Ai or Bi is a string that represents a single variable.

You are also given some queries, where queries[j] = [Cj, Dj] represents the jth query where you must find the answer for Cj / Dj = ?.

Return the answers to all queries. If a single answer cannot be determined, return -1.0.

Note: The input is always valid. You may assume that evaluating the queries will not result in division by zero and that there is no contradiction.

Note: The variables that do not occur in the list of equations are undefined, so the answer cannot be determined for them.

Example 1:

1
2
3
4
5
6
7
Input: equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
Output: [6.00000,0.50000,-1.00000,1.00000,-1.00000]
Explanation: 
Given: a / b = 2.0, b / c = 3.0
queries are: a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ? 
return: [6.0, 0.5, -1.0, 1.0, -1.0 ]
note: x is undefined => -1.0

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
from collections import defaultdict

class Solution:
    def calcEquation(self, equations: List[List[str]], values: List[float], queries: List[List[str]]) -> List[float]:
        graph = defaultdict(list)
        vals = {} # e.g. vals[(a,b)]=2 means a/b=2

        # build bi-directional graph
        for i in range(len(equations)):
            v1, v2 = equations[i]
            graph[v1].append(v2)
            graph[v2].append(v1)
            vals[(v1, v2)] = values[i]
            vals[(v2, v1)] = 1 / values[i]

        # dfs search a path from start to end node
        def dfs(start, end, visited):
            if start in visited:
                return float("inf")

            if start == end:
                return 1

            # mark start node as visited
            visited.add(start)
            res = float("inf")

            for neighbour in graph[start]:
                # e.g. a/c => a/b * b/c
                res = dfs(neighbour, end, visited) * vals[(start, neighbour)]

                # found a path
                if res < float("inf"):
                    break

            return res

        #  calculate each query
        ans = []
        for v1, v2 in queries:
            if v1 not in graph or v2 not in graph:
                ans.append(-1.0)
                continue

            ret = dfs(v1, v2, set())

            if ret == float("inf"):
                ans.append(-1.0)
            else:
                ans.append(ret)

        return ans

[Leetcode 547] Number of Provinces

There are n cities. Some of them are connected, while some are not. If city a is connected directly with city b, and city b is connected directly with city c, then city a is connected indirectly with city c.

A province is a group of directly or indirectly connected cities and no other cities outside of the group.

You are given an n x n matrix isConnected where isConnected[i][j] = 1 if the ith city and the jth city are directly connected, and isConnected[i][j] = 0 otherwise.

Return the total number of provinces.

Example 1:

1
2
3
4
5
6
     1   ---   2

          3

Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output: 2

Solution：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def findCircleNum(self, isConnected: List[List[int]]) -> int:
        n = len(isConnected)
        res = 0
        visited = [False] * n

        # dfs search to explore a province
        def dfs(node, visited):
            visited[node] = True

            for i in range(n):
                if not visited[i] and isConnected[node][i] == 1:
                    dfs(i, visited)

        # dfs search each city and its neighbours. A unvisited city means a new province is formed.
        for i in range(n):
            if not visited[i]:
                res += 1
                dfs(i, visited)
        
        return res

[Leetcode 684] Redundant Connection

In this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.

Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.

Example 1:

1
2
3
4
5
    1 --- 2  
    |  /
    3
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

Example 2:

1
2
3
4
5
   2 --- 1 --- 5
   |     |
   3 --- 4 
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]

Constraints:

  • n == edges.length
  • 3 <= n <= 1000
  • edges[i].length == 2
  • 1 <= ai < bi <= edges.length
  • ai != bi
  • There are no repeated edges.
  • The given graph is connected.

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
from collections import defaultdict

class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        # graph to be constructed
        graph = defaultdict(set)

        # dfs search if a path exists from u to v
        def dfs(u, v):
            # a path is found when to reach the target point v
            if u == v:
                return True

            # mark start point as visited
            visited.add(u)

            # dfs search through each neighbor
            for neighbor in graph[u]:
                if neighbor not in visited and dfs(neighbor, v):
                    return True

            return False

        # add each edge [u,v] to the graph
        for u, v in edges:
            # a new visited is needed for each dfs search from u to v
            visited = set()

            # there exist a path from u to v in the existing graph, the cycle will be formed if new edge [u,v] is added
            if dfs(u, v):
                return [u, v]

            # add edge [u,v] to graph
            else:
                graph[u].add(v)
                graph[v].add(u)

[Leetcode 841] Keys and Rooms

There are n rooms labeled from 0 to n - 1 and all the rooms are locked except for room 0. Your goal is to visit all the rooms. However, you cannot enter a locked room without having its key.

When you visit a room, you may find a set of distinct keys in it. Each key has a number on it, denoting which room it unlocks, and you can take all of them with you to unlock the other rooms.

Given an array rooms where rooms[i] is the set of keys that you can obtain if you visited room i, return true if you can visit all the rooms, or false otherwise.

Example 1:

1
2
3
4
5
6
7
8
Input: rooms = [[1],[2],[3],[]]
Output: true
Explanation: 
We visit room 0 and pick up key 1.
We then visit room 1 and pick up key 2.
We then visit room 2 and pick up key 3.
We then visit room 3.
Since we were able to visit every room, we return true.

Example 2:

1
2
3
Input: rooms = [[1,3],[3,0,1],[2],[0]]
Output: false
Explanation: We can not enter room number 2 since the only key that unlocks it is in that room.

Constraints:

  • n == rooms.length
  • 2 <= n <= 1000
  • 0 <= rooms[i].length <= 1000
  • 1 <= sum(rooms[i].length) <= 3000
  • 0 <= rooms[i][j] < n
  • All the values of rooms[i] are unique.

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:
        visited = [False] * len(rooms)
        visited[0] = True

        def dfs(roomIdx):
            for idx in rooms[roomIdx]:
                if not visited[idx]:
                    visited[idx] = True
                    dfs(idx)

        dfs(0)
        return all(visited)

[Leetcode 1466] Reorder Routes to Make All Paths Lead to the City Zero

There are n cities numbered from 0 to n - 1 and n - 1 roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.

Roads are represented by connections where connections[i] = [ai, bi] represents a road from city ai to city bi.

This year, there will be a big event in the capital (city 0), and many people want to travel to this city.

Your task consists of reorienting some roads such that each city can visit the city 0. Return the minimum number of edges changed.

It’s guaranteed that each city can reach city 0 after reorder.

Example 1:

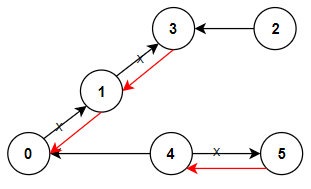
Image

1
2
3
Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
Output: 3
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution:
    def minReorder(self, n: int, connections: List[List[int]]) -> int:
        # create graph with adjacent list
        # mark the connection as 1 if the original connection is from parent to child
        # mark the connection as 0 if the original connection is from child to parent 
        graph = defaultdict(list)
        for conn in connections:
            graph[conn[0]].append((conn[1],1))
            graph[conn[1]].append((conn[0],0))

        print(graph)

        self.count = 0

        # dfs search from root to its subtrees
        def dfs(node, parentVal):
            for childNode in graph[node]:
                childVal = childNode[0]
                parentToChild = childNode[1]

                # only extend the path from parent to child
                if childVal != parentVal:
                    # flip the connection only if original connection is from parent to child
                    self.count += parentToChild

                    # extend the path
                    dfs(childVal, node)

        # treat the graph as a tree rooted with node 0
        dfs(0, -1)
        
        return self.count

BFS

[Leetcode 994] Rotting Oranges

You are given an m x n grid where each cell can have one of three values:

  • 0 representing an empty cell,
  • 1 representing a fresh orange, or
  • 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

Example 1:

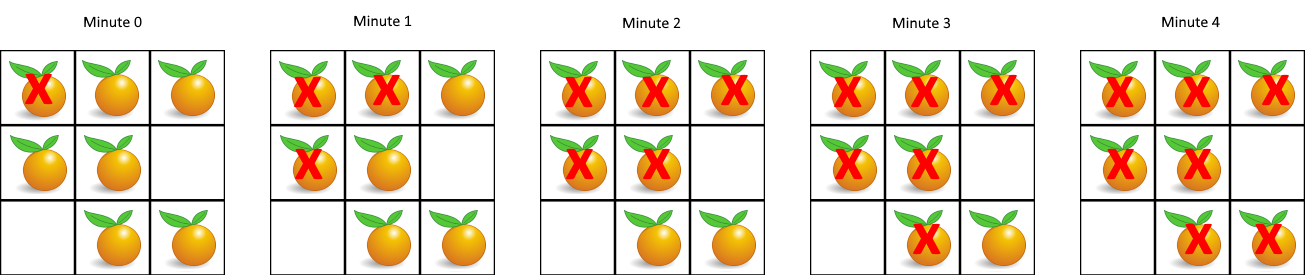
Image

1
2
Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
        # init a queue with rotten oranges
        qu = deque()
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j] == 2:
                    qu.append((i,j))
        
        # 4 directions to rotten
        directions = [(-1,0),(1,0),(0,-1),(0,1)]

        minutes = 0
        while qu:
            # number of rotten oranges
            n = len(qu)

            # rotten fresh oranges very minute
            rotten = False
            for _ in range(n):
                first = qu.popleft()

                # rotten fresh oranges of current rotten orange
                for dx, dy in directions:
                    x, y = first[0] + dx, first[1] + dy
                    if 0 <= x < len(grid) and 0 <= y < len(grid[0]) and grid[x][y] == 1:
                        grid[x][y] = 2 # rotten it
                        qu.append((x,y)) # add the new rotten orange to queue
                        rotten = True # set rotten flag

                # mark current rotten orange as visited
                grid[first[0]][first[1]] = 0

            # add minutes only if there is new rotten oranges
            if rotten:
                minutes += 1

        # check if there is still fresh orange which can't be rotten
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j] == 1:
                    return -1

        return minutes

[Leetcode 1926] Nearest Exit from Entrance in Maze

You are given an m x n matrix maze (0-indexed) with empty cells (represented as ‘.’) and walls (represented as ‘+’). You are also given the entrance of the maze, where entrance = [entrancerow, entrancecol] denotes the row and column of the cell you are initially standing at.

In one step, you can move one cell up, down, left, or right. You cannot step into a cell with a wall, and you cannot step outside the maze. Your goal is to find the nearest exit from the entrance. An exit is defined as an empty cell that is at the border of the maze. The entrance does not count as an exit.

Return the number of steps in the shortest path from the entrance to the nearest exit, or -1 if no such path exists.

Example 1:

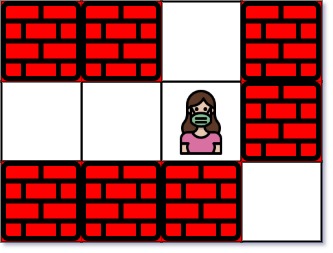
Image

1
2
3
4
5
6
7
8
Input: maze = [["+","+",".","+"],[".",".",".","+"],["+","+","+","."]], entrance = [1,2]
Output: 1
Explanation: There are 3 exits in this maze at [1,0], [0,2], and [2,3].
Initially, you are at the entrance cell [1,2].
- You can reach [1,0] by moving 2 steps left.
- You can reach [0,2] by moving 1 step up.
It is impossible to reach [2,3] from the entrance.
Thus, the nearest exit is [0,2], which is 1 step away.

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution:
    def nearestExit(self, maze: List[List[str]], entrance: List[int]) -> int:
        moves = [(-1,0), (1,0), (0,1), (0,-1)]
        qu = deque()
        qu.append(entrance)
        visited = set(tuple(entrance))  # unhashable type: 'list'

        levels = 0
        while qu:
            # traverse the current level
            levelCells = len(qu)

            for _ in range(levelCells):
                first = qu.popleft()
                currX, currY = first[0], first[1]
                if currX == 0 or currX == len(maze) - 1 or currY == 0 or currY == len(maze[0]) - 1:
                    if maze[currX][currY] == '.' and [currX, currY] != entrance:
                        # found nearest exit
                        return levels

                # bfs search next level(4 directions) for current cell
                for dx, dy in moves:
                    x, y = first[0] + dx, first[1] + dy
                    if  0 <= x < len(maze) and 0 <= y < len(maze[0]) and maze[x][y] == '.' and (x,y) not in visited:
                        visited.add((x,y))
                        qu.append([x,y])

            # move to next level
            levels += 1

        return -1