Backtracking

Posted on Edited on In , Views:

What is backtracking

Backtracking is an algorithmic technique for solving problems recursively by trying to build a solution incrementally, one piece at a time, removing those solutions that fail to satisfy the constraints of the problem at any point in time (by time, here, is referred to the time elapsed till reaching any level of the search tree). Backtracking can also be said as an improvement to the brute force approach. So basically, the idea behind the backtracking technique is that it searches for a solution to a problem among all the available options.

[Leetcode 17] Letter Combinations of a Phone Number

Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent. Return the answer in any order.

A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.

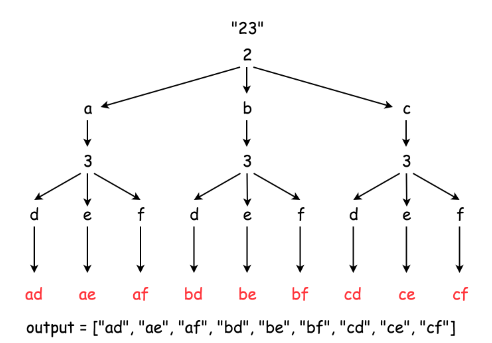
Example 1:

1
2
Input: digits = "23"
Output: ["ad","ae","af","bd","be","bf","cd","ce","cf"]

Example 2:

1
2
Input: digits = ""
Output: []

Example 3:

1
2
Input: digits = "2"
Output: ["a","b","c"]

Constraints:

  • 0 <= digits.length <= 4
  • digits[i] is a digit in the range [‘2’, ‘9’].

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        digitToLetters = {"2":"abc","3":"def","4":"ghi","5":"jkl","6":"mno","7":"pqrs","8":"tuv","9":"wxyz"}
        res = []
        if not digits:
            return res
            
        def getCombinations(s, index, curr):
            if index == len(s):
                res.append(curr)
                return
            
            for letter in digitToLetters[s[index]]:
                getCombinations(s, index + 1, curr + letter)
        
        getCombinations(digits, 0, "")
        return res

[Leetcode 216] Combination Sum III

Find all valid combinations of k numbers that sum up to n such that the following conditions are true:

Only numbers 1 through 9 are used.
Each number is used at most once.
Return a list of all possible valid combinations. The list must not contain the same combination twice, and the combinations may be returned in any order.

Example 1:

1
2
3
4
5
Input: k = 3, n = 7
Output: [[1,2,4]]
Explanation:
1 + 2 + 4 = 7
There are no other valid combinations.

Example 2:

1
2
3
4
5
6
7
Input: k = 3, n = 9
Output: [[1,2,6],[1,3,5],[2,3,4]]
Explanation:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
There are no other valid combinations.

Constraints:

  • 2 <= k <= 9
  • 1 <= n <= 60
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        res = []

        def backtracking(res, ans, currSum, startNum):
            if len(ans) == k:
                # add the answer only if the sum is equal to n
                if currSum == n:
                    res.append(ans[:])

                return

            # always select candiates after the current number to avoid permutations
            # e.g. if [1,2,4] is valid answer, we should NOT include [2,1,4]/ 
            for i in range(startNum, 10):
                # if currSum + i > n, the greater value can be ignored
                if currSum + i > n:
                    break

                ans.append(i) # add to the temporary result
                backtracking(res, ans, currSum + i, i + 1) # recursive call
                ans.pop() # backtracking


        backtracking(res, [], 0, 1)
        return res

[Leetcode 526] Beautiful Arrangement

Suppose you have n integers labeled 1 through n. A permutation of those n integers perm (1-indexed) is considered a beautiful arrangement if for every i (1 <= i <= n), either of the following is true:

  • perm[i] is divisible by i.
  • i is divisible by perm[i].

Given an integer n, return the number of the beautiful arrangements that you can construct.

Example 1:

1
2
3
4
5
6
7
8
9
Input: n = 2
Output: 2
Explanation: 
The first beautiful arrangement is [1,2]:
    - perm[1] = 1 is divisible by i = 1
    - perm[2] = 2 is divisible by i = 2
The second beautiful arrangement is [2,1]:
    - perm[1] = 2 is divisible by i = 1
    - i = 2 is divisible by perm[2] = 1

Example 2:

1
2
Input: n = 1
Output: 1

Constraints:

  • 1 <= n <= 15

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution:
    def countArrangement(self, n: int) -> int:
        self.count = 0

        # find a permutation 
        def findPermuation(n, perm, k):
            if k > n:
                # accumulate to the result
                #print(perm)
                self.count += 1
                return

            # try all the possible elements to construct the permutation
            for p in range(1, n+1):
                # only try the new element which also meets the two requirements
                if (p % k == 0 or k % p == 0) and p not in perm:
                    perm.add(p)
                    findPermuation(n, perm, k+1)
                    perm.remove(p)

            # end early if no element can be found to meet the requirements
            if len(perm) < k:
                return

        findPermuation(n, set(), 1)

        return self.count